Fotografare il cielo: l’astroinseguitore (2a parte)

Prosegue il ciclo dedicato allo studio della tecnologia degli astroinseguitori speriando che possa in futuro suscitare interesse anche presso la Comunità degli autocostruttori italiani.
La fonte principale di questa puntata è ripresa dalla pagina inglese di Wikipedia.

Fig. 1
I vari schemi apparsi su Sky & Telescope nel 1988

Lo scopo di un astroinseguitore è quello di muovere una macchina fotografica con la stessa velocità con cui si muove la volta celeste senza per questo usare, o comprare,  una costosa montatura equatoriale. I motivi di questa scelta possono essere i più disparati: si può immaginare che tra i più comuni vi siano l’ingombro, la facilità di stazionamento, il costo, etc.
L’unica cosa da tenere sempre ben presente è che anche un astroinseguitore richiede il puntamento preciso del suo asse verso il Polo Nord Celeste esattamente come una qualsiasi altra montatura equatoriale da telescopi. 
Non starò a ripetere la storia di questo strumento, per cui come ho promesso, adesso un po’ di teoria. 

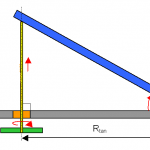Fig. 2 Qui è rappresentato lo schema più semplice, detto a braccio singolo e vite senza fine verticale, o tangente all’asse di rotazione sul cardine. Il problema è che questo schema introduce degli errori nella velocità angolare tanto più ci si discosta lungo la tangente teorica dalla circonferenza immaginaria del cerchio di raggio Rtan. La precisione di inseguimento non supera i 5 – 10 minuti a basse focali (< 50 mm), il che non lo rende affatto adatto per pose a lunga esposizione e grandi obiettivi.

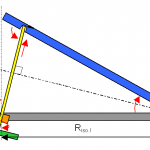Fig. 3 Una parziale soluzione è questa con la vite senza fine montata di sghembo, seguendo una linea secante tra i due vertici della vite e il cerchio immaginario Riso. in questo modo la deviazione tra la velocità angolare dello strumento e la velocità siderale sarà molto ridotta rispetto al primo schema, ma non nulla. La massima deviazione si avrà attorno alla metà corsa della vite per poi di nuovo ridursi verso la fine. Con questa configurazione si possono raggiungere fino a circa 20 minuti di esposizione sempre con basse focali.

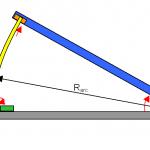
Fig. 4 Come si sarà intuito, la soluzione migliore per uno schema a singolo braccio è quello di curvare la vite secondo una circonferenza di raggio Rarc. In questo modo ogni errore introdotto dalla linearità della vite dei modelli precedenti decade[1]. Con un’accurata sincronia col moto celeste, questa configurazione può virtualmente estendere all’infinito il tempo di esposizione; in pratica, errori nella creazione dell’asta curva e nella velocità dell’asta possono vanificare la bontà di questa soluzione.

Fig. 5 Una novità introdotta nel 1988 da Dave Trott e pubblicata su Sky & Telescope fu la soluzione a doppio braccio, che a fronte di una maggiore complessità di progettazione e realizzazione rispetto ai modelli precedenti qui sopra illustrati, la precisione nell’inseguimento è molte volte superiore, permettendo di ottenere addirittura tempi di esposizione di oltre un’ora.  In sostanza un secondo braccio mobile semplicemente appoggiato al primo consente quel grado di libertà necessario per trasformare il movimento lineare della vite senza fine in movimento circolare su cui appoggia la fotocamera.

Era quel salto qualitativo che gli astrofili che non potevano permettersi una vera montatura equatoriale da tanto attendevano; a quei tempi non erano disponibili reflex a CCD così economiche come oggi e per il profondo cielo si usavano ancora pellicole ed acidi. Era frustrante scoprire che il lavoro di una notte era stato inutile.

Questa tabella mostra l’errore di inseguimento in secondi d’arco calcolata per gli schemi proposti dalla rivista Sky & Telescope nel 1988 e visibili qui all’inizio dell’articolo (Fig. 1).
Il quarto schema  a doppio braccio consente, in via del tutto teorica s’intende, di arrivare fino a 75 minuti di esposizione senza che l’errore apparente superi il secondo d’arco.  Per questo infatti è l’approccio più studiato oltre a quello del braccio singolo e vite curva (Fig. 4), costruttivamente più semplice.

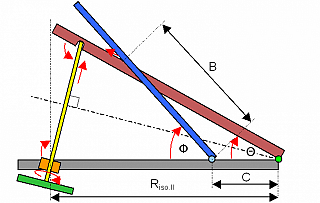
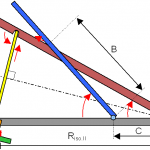
Fig. 5a
R_ISO.II = distanza tra il fulcro del braccio pilota (rosso) e la vite motrice (giallo) lungo la base portante (grigio).
B = distanza tra punto di contatto del braccio pilota con il braccio della fotocamera (blu) e il suo fulcro.
C = distanza tra i fulcri dei due bracci lungo la base portante.

Osserviamo ora in dettaglio la figura 5a che rappresenta uno schema a doppio braccio di tipo 4, il più interessante. In questo schema il braccio pilota nella configurazione a isoscele aziona un secondo braccio su cui è montata la fotocamera. Esperimenti degli astrofili americani su questo schema hanno evidenziato che esistono condizioni particolari in cui l’errore di inseguimento è ridotto al minimo. Queste si ottengono quando il rapporto (che potremo chiamare β) tra la lunghezza del segmento B  e la distanza dei  fulcri rosso e verde (segmento C) è tra 2 e 2,186. L’angolo $\Phi$ attraverso cui il braccio della fotocamera si muove è dato da:
\begin{equation}
\Phi = \Theta+ arcsin \frac{sin\ \Theta}{\beta}
\end{equation}

Fig. 6

La distanza invece tra il fulcro e il braccio motorizzato (rosso) R_ISO.II stabilisce direttamente la velocità di inseguimento del sistema tenendo conto del passo della vite motrice e la sua rotazione espressa in giri al minuto. 
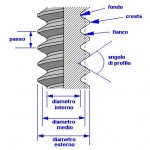
In Europa, dove vale il sistema metrico decimale, il passo (fig. 6) posseduto dalle barre filettate i commercio è espresso in millimetri. Una barra comune spendibile come esempio è la M6, dove 6 sta ad indicare il suo diametro medio, che è di 6 mm e ha il passo di 1,00 mm (vedi tabella).

I motori passo-passo per uso hobbistico sono perfetti per questo tipo di congegni. Un comune NEMA ¹ [2] con micropassi da 0,9° ² è l’ideale per pilotare un astroinseguitore. Si tratta di un motore passo-passo che richiede ben 400 singoli impulsi (360/0,9)  per completare un singolo giro e che quindi può garantire una precisione di movimento molto fine, fino a un quarto di secondo; molto più di quella che si potrebbe richiedere ad un progetto a così basso costo .
Tenendo conto della lunghezza del giorno siderale in minuti e decimali (23h 56m 4,1″), ossia 1436,068, la velocità dell’asta motrice in secondi (supponiamo per semplicità di calcolo di farle compiere un giro in 60 secondi) e il suo passo (in questo caso 1,00 mm), con questa equazione dovremmo ottenere il valore di R_ISO.II:

\begin{equation}\label{eq:Raggio}
 R_{ISO.II}=\frac{\left (  (passo_{vite} *\frac{60}{secondi \times giro}\right )*1436,068}{2\pi}
\end{equation}

\[\rightarrow\]
\begin{equation}
 R_{ISO.II}=\frac{\left (  1,00\ mm * \frac {60}{60}\right ) *1436,068 }{2\pi}= 228,55 \ mm
\end{equation}

A questo punto credo di aver detto molto sulla teoria che sta dietro a questi congegni. Adesso valuterò l’idea per la realizzazione pratica di un astroinseguitore a doppio braccio di tipo 4 come quello descritto in questo articolo. Se avete idee, suggerimenti o critiche, oppure volete dare il vostro aiuto alla realizzazione di questo progetto, vi invito ad usare la form direttamente qui sotto o a scrivere direttamente a : astroinseguitore_at_ilpoliedrico_dot_com. 

[contact-form][contact-field label=’Nome’ type=’name’ required=’1’/][contact-field label=’E-mail’ type=’email’ required=’1’/][contact-field label=’Sito web’ type=’url’/][contact-field label=’Commento’ type=’textarea’ required=’1’/][/contact-form]

 (continua)

Note:

Note:

Riferimenti:

1. "Stepper Motors | Stepper Motors & Controllers"http://www.circuitspecialists.com/stepper-motor